In probability theory, the general[1] form of Bienaymé's identity states that
- .
This can be simplified if are pairwise independent or just uncorrelated, integrable random variables, each with finite second moment.[2] This simplification gives:
- .
The above expression is sometimes referred to as Bienaymé's formula. Bienaymé's identity may be used in proving certain variants of the law of large numbers.[3]
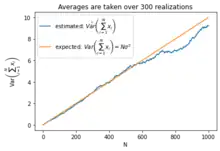
Estimated variance of the cumulative sum of iid normally distributed random variables (which could represent a gaussian random walk approximating a Wiener process). The sample variance is computed over 300 realizations of the corresponding random process.
See also
References
- ↑ Klenke, Achim (2013). Wahrscheinlichkeitstheorie. p. 106. doi:10.1007/978-3-642-36018-3.
- ↑ Loève, Michel (1977). Probability Theory I. Springer. p. 246. ISBN 3-540-90210-4.
- ↑ Itô, Kiyosi (1984). Introduction to Probability Theory. Cambridge University Press. p. 37. ISBN 0 521 26960 1.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.