Zener pinning is the influence of a dispersion of fine particles on the movement of low- and high-angle grain boundaries through a polycrystalline material. Small particles act to prevent the motion of such boundaries by exerting a pinning pressure which counteracts the driving force pushing the boundaries. Zener pinning is very important in materials processing as it has a strong influence on recovery, recrystallization and grain growth.
Origin of the pinning force
A boundary is an imperfection in the crystal structure and as such is associated with a certain quantity of energy. When a boundary passes through an incoherent particle then the portion of boundary that would be inside the particle essentially ceases to exist. In order to move past the particle some new boundary must be created, and this is energetically unfavourable. While the region of boundary near the particle is pinned, the rest of the boundary continues trying to move forward under its own driving force. This results in the boundary becoming bowed between those points where it is anchored to the particles.
Mathematical description
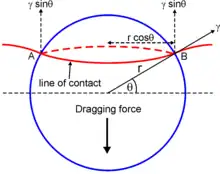
The figure illustrates a boundary intersecting with an incoherent particle of radius . The pinning force acts along the line of contact between the boundary and the particle, i.e., a circle of diameter . The force per unit length of boundary in contact is , where is the interfacial energy. Hence, the total force acting on the particle-boundary interface is
The maximum restraining force occurs when , so .
In order to determine the pinning force resulting from a given dispersion of particles, Clarence Zener made several important assumptions:
- The particles are spherical.
- The passage of the boundary does not alter the particle-boundary interaction.
- Each particle exerts the maximum pinning force on the boundary, regardless of contact position.
- The contacts between particles and boundaries are completely random.
- The number density of particles on the boundary is that expected for a random distribution of particles.
For a volume fraction, , of randomly distributed spherical particles of radius , the number or particles per unit volume (number density) is given by
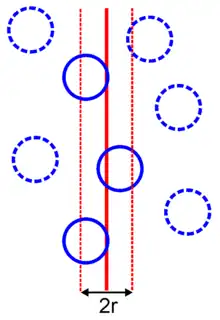
From this total number density, only those particles that are within one particle radius will be able to interact with the boundary. If the boundary is essentially planar, then this fraction will be given by
Given the assumption that all particles apply the maximum pinning force, , the total pinning pressure exerted by the particle distribution per unit area of the boundary is
This is referred to as the Zener pinning pressure. It follows that large pinning pressures are produced by:
- Increasing the volume fraction of particles
- Reducing the particle size
The Zener pinning pressure is orientation dependent, which means that the exact pinning pressure depends on the amount of coherence at the grain boundaries.
Computer Simulation
Particle pinning has been studied extensively with computer simulations, such as Monte Carlo and phase field methods. These methods can capture interfaces with complex shapes and provide better approximations for the pinning force.

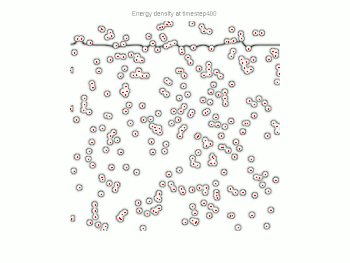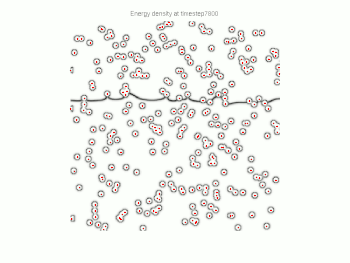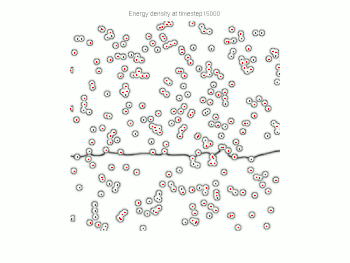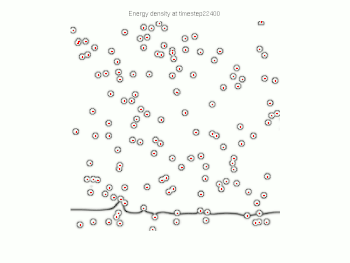
Notes
- According to Current issues in recrystallization: a review, R.D. Doherty et al., Materials Science and Engineering A238 (1997), p 219-274
- For information on zener pinning modeling see:
- "Contribution à l'étude de la dynamique du Zener pinning: simulations numériques par éléments finis", Thesis in French (2003). by G. Couturier.
- "3D finite element simulation of the inhibition of normal grain growth by particles". Acta Materialia, 53, pp. 977–989, (2005). by G. Couturier, R. Doherty, Cl. Maurice, R. Fortunier.
- "3D finite element simulation of Zener pinning dynamics". Philosophical Magazine, vol 83, n° 30, pp. 3387–3405, (2003). by G. Couturier, Cl. Maurice, R. Fortunier.